During the Australian Open, Challenger player (and Youtube star) Karue Sell made a bold statement:

Thank you, Karue, for posting this: It is always valuable to get specific claims about the game from the people who are trying to figure out how to win. Right or wrong, testable propositions like these help nudge our understanding in the right direction.
Now: Right or wrong?
Are second serves becoming mostly useless? A first look at the data says no–or, at least, they aren’t becoming any more useless than they were before. Here is second serve win percentage for tour-level matches since 1991:
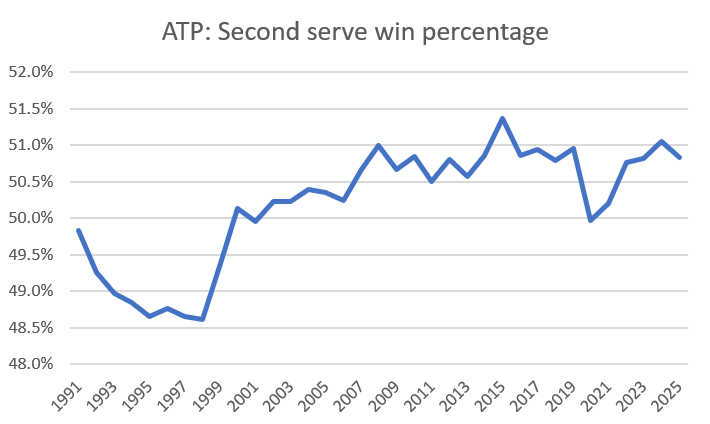
The important thing here isn’t the trend. It’s the narrowness of the values. The difference between the lowest and highest ticks on this graph is only three percentage points, and half of that happened before the century turned. Strength and strategy may be different–we’ll get to that–but the results aren’t. If anything, second serves have become (modestly) less useless.
This trend holds up even when we tweak the parameters. Yes, the surface mix of the tour has changed since the 1990s. But if we look only at hard-court matches, there’s an even tighter range of yearly averages, between 48.9% and 51.2%. At Sell’s Challenger level, I only have data back to 2010. In that span, hard-court second-serve win rates have drifted less than a single percentage point, between 49.7% and 50.6%.
I can’t help but notice that Sell’s own Challenger-level second-serve win percentage is a healthy 52%. I’m sure it sometimes feels useless: The last match he played before making the comment was a qualifying-round loss in which he salvaged less than 40% of second-serve points. But despite his relatively small stature, he won more main draw second-serve points last year than Matteo Berrettini did–albeit against weaker competition.
Risk and reward
No one wants to settle for historical average. Inevitably, someone brought up the notion of two first serves:
No, two first serves are not the way. But Sell recognizes what might work. At least in theory, players should take more risk on second serves (and perhaps on firsts, as well), hitting bigger and winning more points at the cost of more doubles.
If tennis trends proceeded by opinion poll, I think we’d already see evidence of this. I certainly never see anyone argue that players should be more conservative with the second ball, unless they’re talking about a particular struggling player. But all that matters is what happens on court, and there’s no sign there of more double faults:
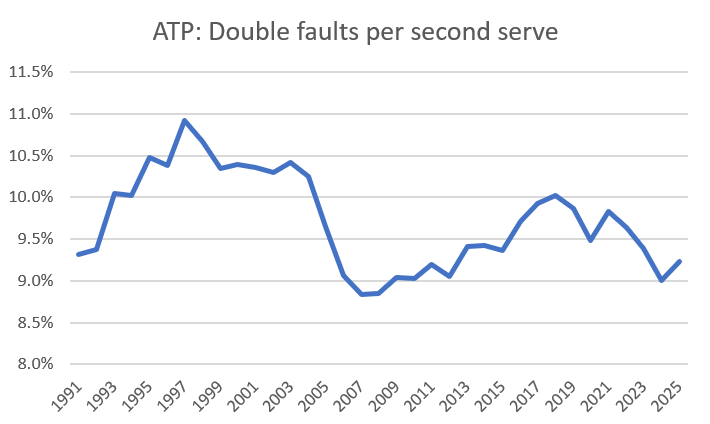
Again, the framing doesn’t matter. The numbers are about the same regardless of surface, and Challenger players have moved in the same direction. In fact, the 2025 Challenger rate so far is 9.8%, the first time that the minor leaguers have dipped below double digits.
To be clear, I wouldn’t expect any sudden moves here. A generation of players grows up learning certain serves and tactics, and there’s only so much they can do to change them. An equation might spit out that someone would win, say, 56% of second-serve points in exchange for accepting a 12% double-fault rate. But do athletes really have such fine-grained control of the risks they take? I suspect not, which means another generation may go by before we see a true “1 and 1.5” strategy.
Is 100 miles per hour a must?
How fast do second serves need to be? While I can’t imagine any player would turn down a triple-digit average, we’re nowhere near that level. The rightmost column shows the average second-serve speeds at the 2024 US Open for every player who reached the third round:
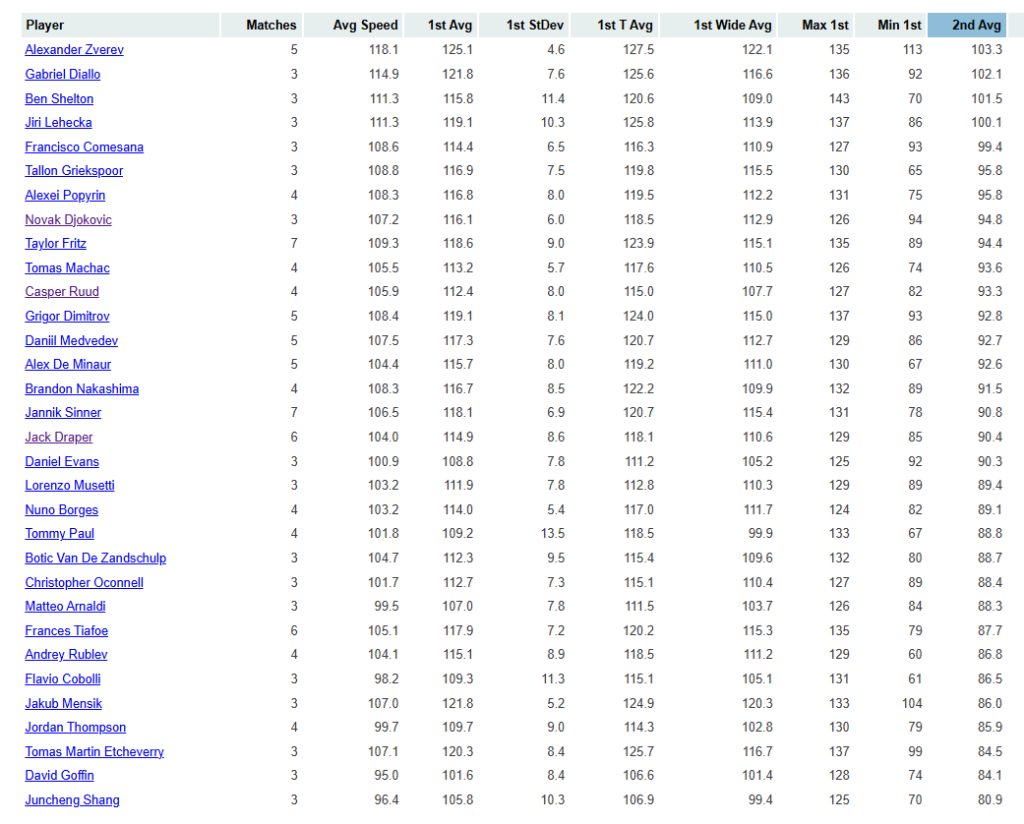
Only 4 of 32 averaged triple digits. Just five posted a mark at or above 96 miles per hour. The dominant tournament winner, Jannik Sinner, barely topped 90.
It’s possible that the sensors (or the balls, or the humid conditions, or pick your variable) resulted in low readings: US Open speeds are typically several miles per hour lower than Wimbledon speeds, even for the same players. But the gap isn’t enough to push more than a quarter of these guys over the magic number.
Still, Sell could be correct on the trend, if not on the detail. Maybe second serves are getting faster, or slower second serves are more likely to end in a point lost.
US Open data, though, suggests that second serves have stayed about the same. I have relevant data back to 2014, plus 2011. Splitting second serves into buckets of 100-plus miles per hour, 95-99, 90-94, and so on, it’s tough to find much of a trend:
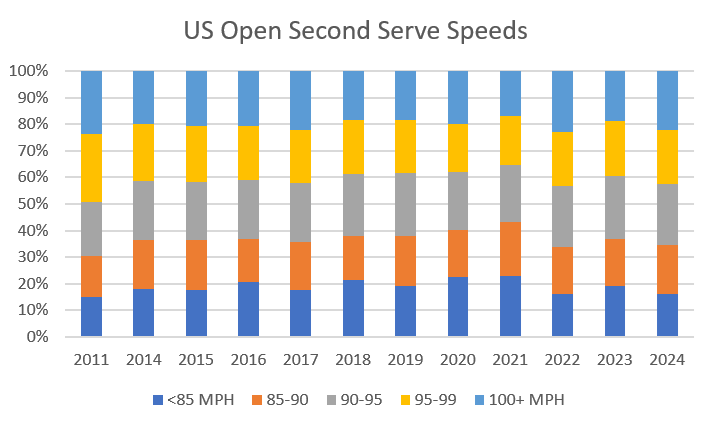
(In case you’re wondering, the 2012-13 data has serve speeds, but no indication of first or second serves. Not very helpful here!)
Same story with win rates. As with the tour in general, the US Open has seen a steady percentage of second-serve points won. The next graph shows year-by-year win rates both overall and for the 85-89 mile-per-hour bucket, on the theory that if returners were feasting on relatively weak seconds, it would show up there:
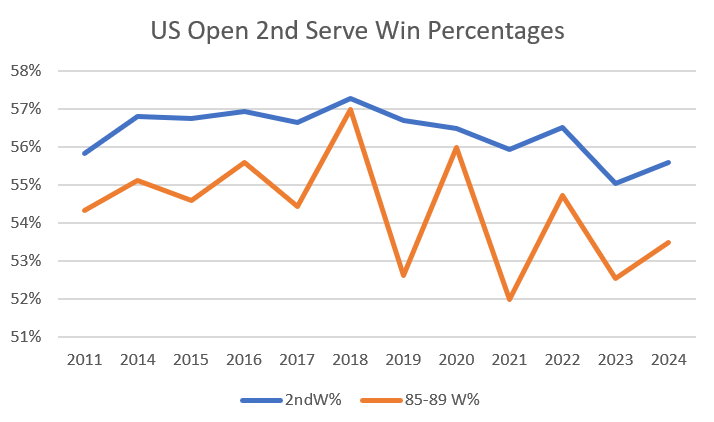
While the 85-89 mph results are noisy, there’s not much to see here. The overall win rate in 2024 is almost identical to what it was 13 years earlier. There’s a bit of space between 85-89 mph second serves in 2011 and 2024, but still not much.
It’s certainly true that harder is better, and that hasn’t changed. At every one of these US Opens, the win rate of 100-plusses exceeded the win rate of sub-85s by at least five percentage points, and the gap rose as high as ten points at the 2020 Covid event. But we’ve yet to find much evidence for the notion that second serve speeds or results are any different than they were 10, 13, or even 30 years ago.
Are servers going to the forehand more often?
Finally, we can say… maybe?
I pulled all hard court matches since 2014 between right-handers from the Match Charting Project database. (Hard court, because it’s so much easier to run around second serves on clay; 2014, because that’s when the project started, so there’s not as much bias toward big-name players and matches; right-handers, because lefties, while fascinating, make things way more complicated.)
The charts classify serves into three categories: Wide, body, and T. Second serves to the “body” usually aren’t good: Those are serves that didn’t find a corner. In the men’s game, that’s 35-40% of seconds. It’s tough to tell from the chart–and sometimes even when watching a match–exactly which side the server targeted, because it is so easy for the returner to take a step or two around it and hit a forehand.
Servers are indeed more likely these days to find the forehand corner:
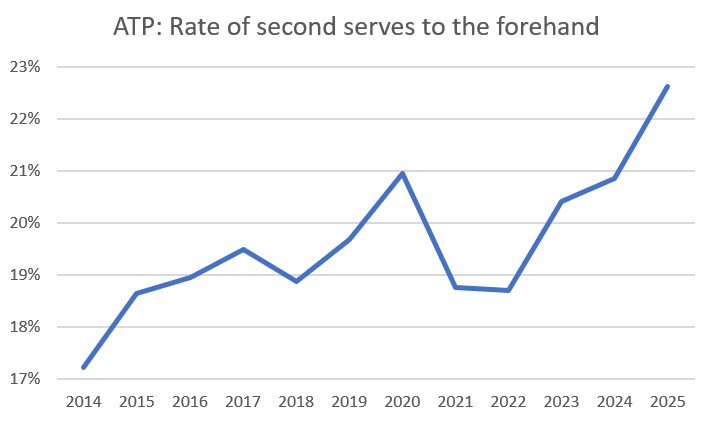
This isn’t an enormous move, but it seems like a real thing. If we throw out the 2020 Covid season, it would look like an even more dramatic shift just in the last few years.
However, more second serves to the forehand corner does not mean fewer second serves to the backhand corner. These extra forehand-targeted serves are coming at the expense of the mediocre “body” seconds. Servers drill the backhand corner 30% to 35% of the time, and that range hasn’t budged over the last decade.
I’d more inclined to say, then, that players have gotten a bit better. And they’ve chosen to use that improvement to keep returners off balance, aiming a few more second serves to the forehand side.
Are players too good from the back?
Sell’s theory is that more second serves are targeting the forehand, because the backhand is no longer such a weak side. We can use the same subset of MCP data to check how (right-handed) returners have fared against second serves to their backhand corner:
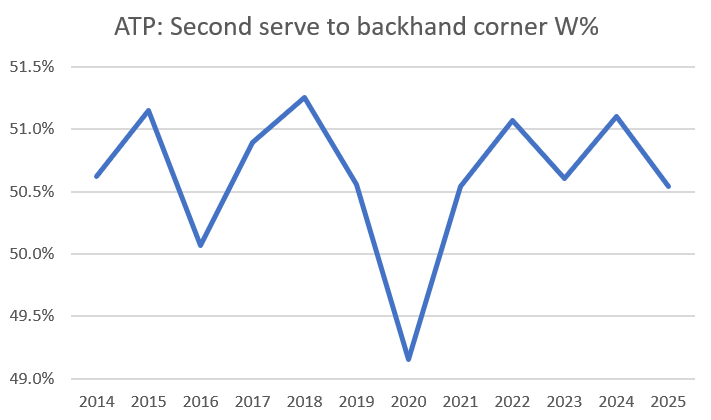
Again, 2020 is weird; other than that, we’re just looking at noise. (Or, possibly, the signature of a drunk blue M&M.) The long-term average of this stat is 50.6%, and in ten of the twelve seasons, the single-year number was within half a percentage point of that.
Backhand returns may have gotten stronger, but if so, serves are advancing at the same rate.
What gives?
Why would Karue identify trends that, for the most part, have so little evidence to support them?
First, the tour is getting stronger, at backhand returns and everything else. Some serves that would’ve gone unreturned in 2005 or 2015 are coming back today. As we’ve seen, servers are maintaining a balance. But it’s easy to suffer a few bad results and conclude that drastic changes have taken place.
Second, Karue himself played his best tennis last year. He cracked the top 300 for the first time and played a dozen Challenger main draws. That meant he faced stronger competition than ever. The Challenger tour is full of baseline battlers with sturdy backhands; there isn’t a huge gap between the return skill that Sell faces these days and the elite-level returning we watch on TV. Moving up from ITFs to Challengers means that some weapons don’t work anymore, and–especially for smaller guys–new tactics are needed.
I’d love to see Sell, or anyone else, give a serious trial to the “1 and 1.5” serve strategy. Hit seconds harder, attack the forehand more often, and accept more double faults. Karue might be right about what the future of second serves will look like, but we’re not there yet.
* * *
Subscribe to the blog to receive each new post by email: